網友Tianba提供了一篇網絡上的測試簡報,覺得很棒,先在此探討此文的內容,有時間,再來談交易上的應用與問題.

這是簡報的原始網址:

http://research.cs.tamu.edu/prism/lectures/iss/iss_l13.pdf

這篇簡報,名為測試(Validation),分為四個部分來討論.

中文的測試,涵蓋的相當廣,容易造成誤解.這篇簡報的原文,叫做Validatation,指的是有效性的測試.一般計算機程序的測試,指的是Verification,專門測試與解決程序撰寫時所產生的問題.Verify動作在前,Validate在后.

以下是用中文來整理這篇簡報

    第一部分,談到的是測試的動機(Motivation):

有效性測試,處理模式識別上(pattern recognition)的兩個基本問題:

    模型選擇(Model selection):

    幾乎所有的模式識別技術,都會有一個或多個自由參數(free parameters),如

      kNN分類法(kNN Classification Rule)中的鄰近數(Number of neighbors),

      MLPs方法的網絡數(network size),學習參數(learning parameters)與加權(weights).

    要如何針對特定的分類問題(given classification problem)中,選擇"最佳"參數或模型呢?  

    績效估計(Performance estimation):

    一旦選擇了模型,要怎樣來估計績效呢?傳統上,績效的測量是采用真實誤差率(True Error Rate),采用的分類(Classifier)與要處理的真實母體之間,所存在的誤差率.(X5super注: 此并非母體的績效高低,而是估計準確度,如果100分,誤差率0.2,那母體只有80分,如果90分,誤差率0,那母體就是90分了.前者的分數雖然較高,但是誤差率高,估計就過于樂觀.若以程序交易為例,這只是評估回測的可靠度,不管策略本身的績效好壞)

    假如我們沒有取樣數的限制,這些問題就有了直接的答案:取最低的母體誤差率(Error Rate on Entire Population),當然,這時候就等于真實誤差率(True Error Rate).（ www.kzuj.com.cn ）

    在實際的應用上,我們只能用有限的取樣數,而且通常都比我們想要的還小.一種做法是,把所有的數據(trainning data),只當成一個分類(Classifier),并以此來估計誤差率.這樣,產生了兩個主要問題:

    問題1) 最終選定的模型會過度匹配于我們使用的數據(trainning data),如果模型的參數越多,問題就更顯著.

    問題2) 誤差率的估計,會太過于樂觀(低于True Error Rate).事實上,要取得學習資料(Trainning data)100%正確率的分類(classification),不是不尋常的事.(X5super注:這樣的估計太過于樂觀)

    另一個更好的做法是,holdout method:把學習數據(trainning data)分割為更多互不交集的區塊(disjoint subsets).

    第二部分: holdout method

    切割后的區塊(dataset),有兩類:學習組(Trainning set),用來找分類(Classifier)的模型;另一類是測試組(Test set)用來評估這分類(classifier)的誤差率.

    hold method 的典型應用,在反向傳播誤差(back propagation error)的停止點決策.

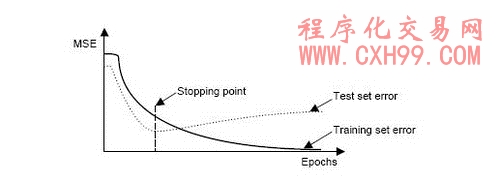
    這個方法有兩個缺點:一是通常我們擁有的數據不多,無法在做這樣奢華的切割后,還有測試的能力與價值;另一個是,只切割成為一組的學習與測試數據,一旦我們不幸選擇了不具代表性的那個組合,結果的誤差率計算就沒有估計的意義與價值了.

    這樣的限制,是有一些重復取樣的方法族群(family of resampling methods)可以克服的,這些方法需要更多的計算過程.比如交互驗證法(Cross Validation):隨機子取樣(random subsampling),K-Fold交互驗證,Leave-One-Out交互驗證.另外,還有BootStrap(引導)方法.

    第三部分: Re-sampling techniques

    A) Random subsampling:

       將數據分割為K組.首先,隨機決定K個號碼小于總樣本數,這些號碼不重復,每個號碼代表每一個分割的最終樣本數.在每一個分割中,學習數據組(trainning samples),帶入模型參數,測試數據組(test samples)估計誤差率.

       總共產生K組的估計,最后的誤差估計值E=ΣEi/K,顯著的比holdout method單組估計好很多.

    B) K-Fold Cross Validation:

       建立K格位的數據組,也就是把所有的測試數據等分成K組:第K次的試驗(experiments),采用前面K-1組的數據來學習(trainning),第K組的數據來測試(testing)

        
       此法與random subsampling類似.K-Fold Cross Validataion的優點,是每一個取樣數據,最后都扮演過學習(trainning)與測試(testing)的腳色.

       績效估計如同前者,誤差估計值E=ΣEi/K.

    C) Leave-One-Out Cross Validation:

       這是K-Fold Validation的一種退化變形,總數據樣本數就是K個.

       當樣本數N個,就采取N個試驗(experiments).第N次試驗,采用前面N-1個的樣本數據來學習(trainning),第N個樣本數數據來試驗(testing).         

       同樣的,真實誤差的估計=E=ΣEi/N.

       有一個有意思的問題,到底數據要折迭多少個分割(folds)呢?

       A)當數量大:

          (+有利):真實誤差估計的偏差會很小(估計會接近正確)

          (-不利):真實誤差估計的變異會很大

          (-不利):計算時間長

       B)當數量小:

          (有利):計算時間短

          (有利):真實誤差估計的變異小

          (不利):真實誤差估計的偏差會很大

       實務上,Folds的數量取決于擁有的樣本數據數.當資料數夠多,即使3-Fold Cross Valiation,也能有相當正確的估計.當數據數少,最好使用Leave-One-Out Cross Validation,盡量讓試驗數夠多.

       K-Fold Cross Valiation一般的用法是K=10.

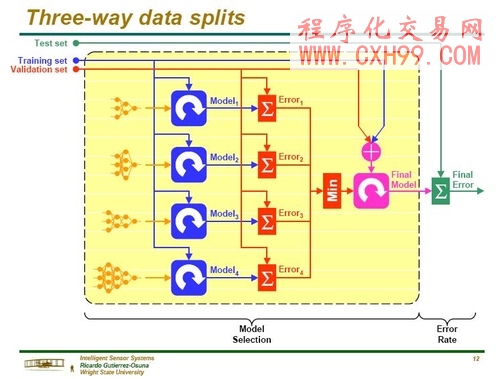
    第四部份: 數據三類別切割法(Three-Way data split)

    假如模型的選定與真實誤差率的估計要同時算出,那么數據需要分割成互不交集的三部分.

    學習區(Trainning set):模型形成(learning)之用,讓模型的參數符合這個分類(classifier).前面提到的MLP方法,在使用back-prop rule時,這學習區可以去尋找"最佳"的權數(weights).

    修正區(Validation set):用來微調參數.MLP方法在使用back Propagation算法時,修正區可以用來尋找"最佳隱藏單元的數量(number of hidden units),或決定停止點(stopping point)

    測試區(test set):只用來評估完全學習結束后的分類(classifier)績效.(真實誤差率).MLP方法在此已經選定了最終模型后(MLP size與實際權重),將估計模型誤差率.在最終模型績效估計后,不可再修改參數值了.

    把修正區(validation set)從測試區(test set)分離出來,有兩個理由:一是合并選定模型與估計績效在同一區的話,會低估誤差率;另一個就是前面提過的,在最終模型績效估計后,不可再修改參數值了.

    步驟綱要:

    1) 將可用的數據,分成學習(trainning set),修正(validation set)與測試(test set)三部分.

    2) 選定架構(architecture)與參數

    3) 用學習區(tranning set)的數據,讓模型學習形成.

    4) 用修正區(validation set)的數據,來評價(evaluate)模型.

    5) 用不同的架構與學習參數,重復步驟2~4.

    6) 選定模型,并且用學習區與修正區的數據來學習

    7) 用測試數據(test set),來評估(assess)最后的模型.

    以上的步驟是假設用holdout method.如果用的是Cross Validation或Bootstrap方法,對于K folds中的每一個,都要重復步驟3與4.